\tfrac, \dfrac, \cfrac und \genfrac aus dem amsmath PaketDas amsmath Paket erweitert die Funktionalitäten von LaTeX um zahlreiche mathematische Befehle. Zu diesen gehören \tfrac, \dfrac, \cfrac und \genfrac, die für die Darstellung von Brüchen verwendet werden. Im Folgenden werden diese Befehle im Detail beschrieben.
\tfracDer Befehl \tfrac steht für "text fraction" und erzeugt einen Bruch im Textmodus, der kleiner und kompakter als der Standardbruch ist. Er ist nützlich, wenn Brüche innerhalb von Textzeilen dargestellt werden sollen, ohne die Höhe der Zeile stark zu verändern.
\tfrac{Zähler}{Nenner}
Die Formel lautet $\tfrac{a}{b} + \tfrac{c}{d}$.
In diesem Beispiel werden die Brüche $\tfrac{a}{b}$ und $\tfrac{c}{d}$ in einer kompakten Form innerhalb einer Textzeile dargestellt.
\dfracDer Befehl \dfrac steht für "display fraction" und erzeugt einen Bruch im Display-Modus, auch wenn er im Textmodus verwendet wird. Dies führt zu einem größeren Bruch, der besser lesbar ist, insbesondere bei komplexen Ausdrücken.
\dfrac{Zähler}{Nenner}
Die Formel lautet $\dfrac{a}{b} + \dfrac{c}{d}$.
In diesem Beispiel werden die Brüche $\dfrac{a}{b}$ und $\dfrac{c}{d}$ in einer größeren und besser lesbaren Form dargestellt, selbst wenn sie im Textmodus verwendet werden.
\cfracDer Befehl \cfrac steht für "continued fraction" und wird verwendet, um Kettenbrüche darzustellen. Ein Kettenbruch ist ein Bruch, bei dem der Nenner selbst wieder ein Bruch ist, und so weiter.
\cfrac{Zähler}{Nenner}
Ein Kettenbruch kann wie folgt dargestellt werden: $\cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{4}}}$.
In diesem Beispiel wird der Kettenbruch $\cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{4}}}$ dargestellt, wobei jeder Nenner wieder ein Bruch ist.
\genfracDer Befehl \genfrac steht für "generalized fraction" und bietet eine hohe Flexibilität bei der Erstellung von Brüchen. Mit \genfrac können verschiedene Parameter wie Linienart und Stil des Bruchstrichs sowie die Größe des Bruchs angepasst werden.
\genfrac{LinkerDelimiter}{RechterDelimiter}{Linienbreite}{Stil}{Zähler}{Nenner}
LinkerDelimiter: Zeichen, das links vom Bruch erscheinen soll (z.B. (, {, [, etc.)RechterDelimiter: Zeichen, das rechts vom Bruch erscheinen soll (z.B. ), }, ], etc.)Linienbreite: Breite des Bruchstrichs (0 für keinen Bruchstrich, 1 für normalen Bruchstrich, -1 für keinen Strich und - andere Werte für unterschiedliche Dicken)Stil: Stil des Bruchs (\displaystyle für Display-Stil, \textstyle für Text-Stil, \scriptstyle für kleineren Stil, \scriptscriptstyle für noch kleineren Stil)Zähler: Zähler des BruchsNenner: Nenner des BruchsDie allgemeine Form eines Bruchs kann mit $\genfrac{}{}{0pt}{}{\alpha}{\beta}$ dargestellt werden.
In diesem Beispiel wird der Bruch $\genfrac{}{}{0pt}{}{\alpha}{\beta}$ ohne linke und rechte Delimiter, ohne Bruchstrich und im Text-Stil dargestellt.
Die fehlenden Größenanpassungen, für scriptstyle und scriptscriptstyle, lassen sich über den Befehl genfrac selbst erstellen.
\newcommand{\sfrac}{\genfrac{}{}{}2}
\newcommand{\ssfrac}{\genfrac{}{}{}3}
$\sfrac{a}{b}$ und $\ssfrac{a}{b}$ 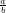 und
und
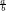
Diese vier Befehle des amsmath Pakets ermöglichen es, Brüche in unterschiedlichen Größen und Stilen darzustellen, je nach den Anforderungen des mathematischen Ausdrucks:
\tfrac: Kompakter Bruch im Textmodus.\dfrac: Großer Bruch im Display-Modus.\cfrac: Darstellung von Kettenbrüchen.\genfrac: Allgemeine und flexible Brucherstellung mit verschiedenen Parametern.Die Wahl des richtigen Befehls hängt vom Kontext ab, in dem der Bruch dargestellt werden soll, sowie von der gewünschten Darstellung und Lesbarkeit.