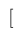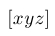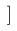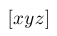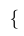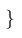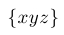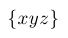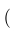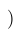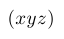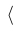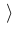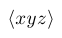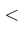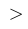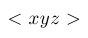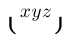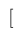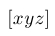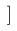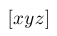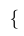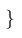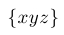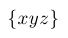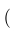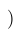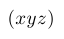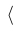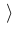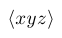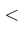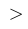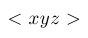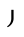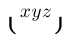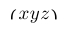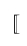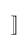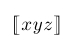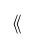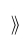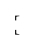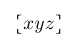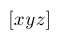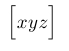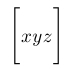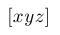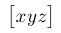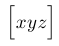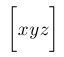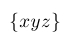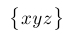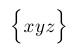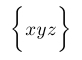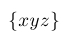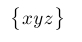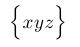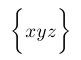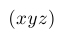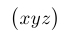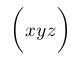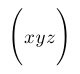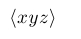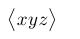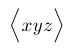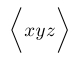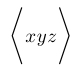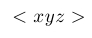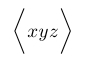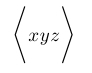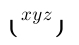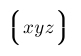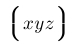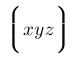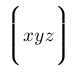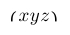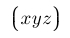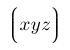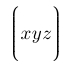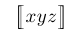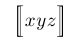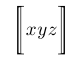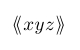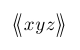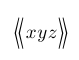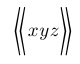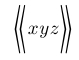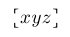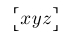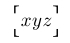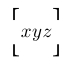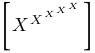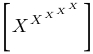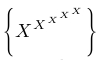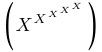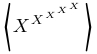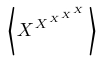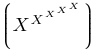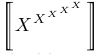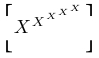LaTeX Klammern
In LaTeX gibt es verschiedene Arten von Klammern, die in mathematischen Ausdrücken verwendet werden können. Dieser Abschnitt behandelt die verschiedenen Klammernarten, die sowohl ohne zusätzliche Pakete als auch mit speziellen Paketen genutzt werden können.
Standard Klammern
Standard Klammern können ohne die Notwendigkeit zusätzlicher Pakete verwendet werden. Sie eignen sich sowohl für Inline-Mathematik als auch für abgesetzte mathematische Ausdrücke.
Hinweis: Die Befehle \[ ... \] und \( ... \) sind Abkürzungen für \begin{displaymath} ... \end{displaymath} bzw. \begin{math} ... \end{math}.
Standard Klammern
Standard bedeutet, dass die Befehle ohne zusätzliches Paket genutzt werden können.
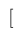 | $ [ $ |
 | $ ] $ |
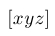 | $[ xyz ]$ |
 | $\lbrack$ |
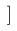 | $\rbrack$ |
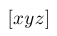 | $\lbrack xyz \rbrack$ |
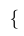 | $ \{ $ |
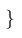 | $ \} $ |
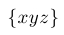 | $\{ xyz \}$ |
 | $\lbrace$ |
 | $\rbrace$ |
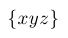 | $\lbrace xyz \rbrace$ |
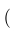 | $ ( $ |
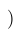 | $ ) $ |
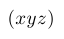 | $( xyz )$ |
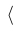 | $\langle$ |
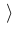 | $\rangle$ |
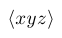 | $\langle xyz \rangle$ |
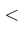 | $ < $ |
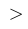 | $ > $ |
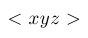 | $< xyz >$ |
 | $\lgroup$ |
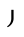 | $\rgroup$ |
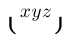 | $\lgroup xyz \rgroup$ |
Mn Symbol
Einige spezielle Klammerarten sind nur mit dem Paket MnSymbol verfügbar. Diese Klammern bieten zusätzliche Typen und Stile für mathematische Ausdrücke. Diese Klammertypen sind erst mit dem Paket MnSymbol verfügbar.
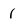 | $\lgroup$ |
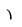 | $\rgroup$ |
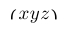 | $\lgroup xyz \rgroup$ |
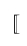 | $\lsem$ |
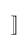 | $\rsem$ |
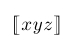 | $\lsem xyz \rsem$ |
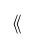 | $\llangle$ |
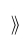 | $\rrangle$ |
 | $\llangle xyz \rrangle$ |
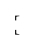 | $\ullcorner$ |
 | $\ulrcorner$ |
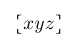 | $\ullcorner xyz \ulrcorner$ |
feste Größe
Klammern können auch in fester Größe definiert werden, was besonders nützlich ist, wenn die Größe der Klammern unabhängig von ihrem Inhalt sein soll.
eckige Klammern
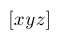 | $[ xyz ]$ |
 | $\bigl[ xyz \bigr]$ |
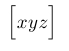 | $\Bigl[ xyz \Bigr]$ |
 | $\biggl[ xyz \biggr]$ |
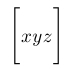 | $\Biggl[ xyz \Biggr]$ |
brack (eckige) Klammern
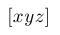 | $\lbrack xyz \rbrack$ |
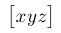 | $\bigl\lbrack xyz \bigr\rbrack$ |
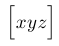 | $\Bigl\lbrack xyz \Bigr\rbrack$ |
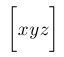 | $\biggl\lbrack xyz \biggr\rbrack$ |
 | $\Biggl\lbrack xyz \Biggr\rbrack$ |
geschweifte Klammern
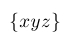 | $\{ xyz \}$ |
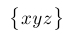 | $\bigl\{ xyz \bigr\}$ |
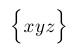 | $\Bigl\{ xyz \Bigr\}$ |
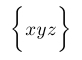 | $\biggl\{ xyz \biggr\}$ |
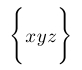 | $\Biggl\{ xyz \Biggr\}$ |
brace (geschweifte) Klammern
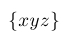 | $\lbrace xyz \rbrace$ |
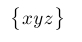 | $\bigl\lbrace xyz \bigr\rbrace$ |
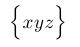 | $\Bigl\lbrace xyz \Bigr\rbrace$ |
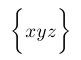 | $\biggl\lbrace xyz \biggr\rbrace$ |
 | $\Biggl\lbrace xyz \Biggr\rbrace$ |
runde Klammern
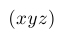 | $( xyz )$ |
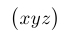 | $\bigl( xyz \bigr)$ |
 | $\Bigl( xyz \Bigr)$ |
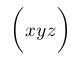 | $\biggl( xyz \biggr)$ |
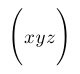 | $\Biggl( xyz \Biggr)$ |
angle (spitze) Klammern
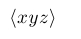 | $\langle xyz \rangle$ |
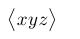 | $\bigl\langle xyz \bigr\rangle$ |
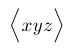 | $\Bigl\langle xyz \Bigr\rangle$ |
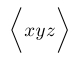 | $\biggl\langle xyz \biggr\rangle$ |
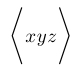 | $\Biggl\langle xyz \Biggr\rangle$ |
spitze Klammern
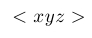 | $< xyz >$ |
 | $\bigl< xyz \bigr>$ |
 | $\Bigl< xyz \Bigr>$ |
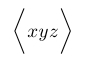 | $\biggl< xyz \biggr>$ |
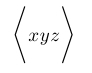 | $\Biggl< xyz \Biggr>$ |
group Klammern
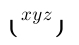 | $\lgroup xyz \rgroup$ |
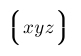 | $\bigl\lgroup xyz \bigr\rgroup$ |
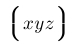 | $\Bigl\lgroup xyz \Bigr\rgroup$ |
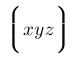 | $\biggl\lgroup xyz \biggr\rgroup$ |
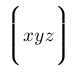 | $\Biggl\lgroup xyz \Biggr\rgroup$ |
Mn Symbol
group Klammern
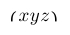 | $\lgroup xyz \rgroup$ |
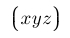 | $\bigl\lgroup xyz \bigr\rgroup$ |
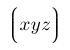 | $\Bigl\lgroup xyz \Bigr\rgroup$ |
 | $\biggl\lgroup xyz \biggr\rgroup$ |
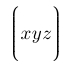 | $\Biggl\lgroup xyz \Biggr\rgroup$ |
sem Klammern
 | $\lsem xyz \rsem$ |
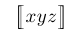 | $\bigl\lsem xyz \bigr\rsem$ |
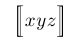 | $\Bigl\lsem xyz \Bigr\rsem$ |
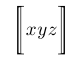 | $\biggl\lsem xyz \biggr\rsem$ |
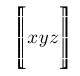 | $\Biggl\lsem xyz \Biggr\rsem$ |
angle Klammern
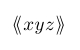 | $\llangle xyz \rrangle$ |
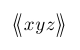 | $\bigl\llangle xyz \bigr\rrangle$ |
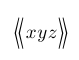 | $\Bigl\llangle xyz \Bigr\rrangle$ |
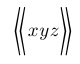 | $\biggl\llangle xyz \biggr\rrangle$ |
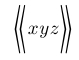 | $\Biggl\llangle xyz \Biggr\rrangle$ |
corner Klammern
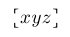 | $\ullcorner xyz \ulrcorner$ |
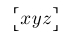 | $\bigl\ullcorner xyz \bigr\ulrcorner$ |
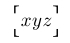 | $\Bigl\ullcorner xyz \Bigr\ulrcorner$ |
 | $\biggl\ullcorner xyz \biggr\ulrcorner$ |
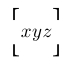 | $\Biggl\ullcorner xyz \Biggr\ulrcorner$ |
variable Größe / flexible Größe
Durch die Verwendung der Befehle \left und \right passen sich die Klammern automatisch an die Höhe des umschlossenen Ausdrucks an. Dies ist besonders nützlich bei sehr großen oder komplexen Ausdrücken, bei denen die Höhe nicht vor dem Setzen der Formel bekannt ist.
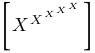 | $\left[ X^{X^{X^{X^{X}}}} \right]$ |
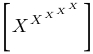 | $\left\lbrack X^{X^{X^{X^{X}}}} \right\rbrack$ |
 | $\left\{ X^{X^{X^{X^{X}}}} \right\}$ |
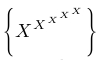 | $\left\lbrace X^{X^{X^{X^{X}}}} \right\rbrace$ |
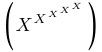 | $\left( X^{X^{X^{X^{X}}}} \right)$ |
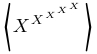 | $\left\langle X^{X^{X^{X^{X}}}} \right\rangle$ |
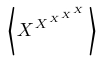 | $\left< X^{X^{X^{X^{X}}}} \right>$ |
MnSymbol
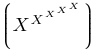 | $\left\lgroup X^{X^{X^{X^{X}}}} \right\rgroup$ |
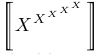 | $\left\lsem X^{X^{X^{X^{X}}}} \right\rsem$ |
 | $\left\llangle X^{X^{X^{X^{X}}}} \right\rrangle$ |
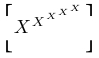 | $\left\ullcorner X^{X^{X^{X^{X}}}} \right\ulrcorner$ |