Innerhalb von LaTeX gibt es verschiedene Möglichkeiten, um Matrizen und Vektoren zu setzen. Im Folgenden werden Befehle und Möglichkeiten zur Darstellung von Matrizen und Vektoren in LaTeX gezeigt.
Innerhalb des Standards gibt es dafür keinen eigenen Befehl und auch keine eigene Umgebung. Hier ist man auf die Verwendung der array-Umgebung angewiesen, wenn man eine Matrix oder einen Vektor setzen will. Dabei müssen aber zwei Dinge beachtet werden: Zum einen muss, wie bei einer Tabelle, die Anzahl und die Ausrichtung der benötigten Spalten vorab festgelegt und gesetzt werden. Und zum anderen fehlt der array-Umgebung die typische Klammerung, die eine Matrix einfasst. Diese muss zusätzlich um die Matrix herum gesetzt werden. Als Beispiel für die Darstellung von Matrizen wird hier die Einheitsmatrix verwendet, da deren Aufbau allgemein bekannt sein dürfte.
Eingabe:
$\begin{array}{rrrr}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}$
Ausgabe:
$\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}$An diesem einfachen Beispiel erkennt man bereits das Problem mit der Klammerung und dass die Spalten vorab definiert werden müssen. Die Klammern lassen sich mit den Befehlen \left und \right einfügen, wie die nachfolgenden Beispiele zeigen. Bei den Klammersymbolen ist darauf zu achten, dass es sich um ein druckbares Zeichen handelt beziehungsweise, wenn es ein Sonderzeichen wie die geschweiften Klammern {, } ist, das Zeichen maskiert wird.
Eingabe:
$\left( \begin{array}{rrrr}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}\right) $
$\left[ \begin{array}{rrrr}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}\right] $
Ausgabe:
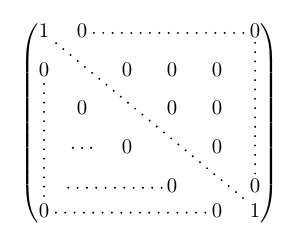
$\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right) $ $\left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right] $Mittels der Befehle \cdots, \ddots und \vdots sind auch Auslassungen, d.h. Pünktchen, innerhalb der Matrix zwischen den Spalten und Zeilen möglich.
Eingabe:
$\left( \begin{array}{rrrr}
1 & 0 & \cdots & 0 \\
0 & \ddots & 0 & \vdots \\
\vdots & 0 & \ddots & 0 \\
0 & \cdots & 0 & 1 \\
\end{array}\right) $
Ausgabe:
$\left( \begin{array}{rrrr} 1 & 0 & \cdots & 0 \\ 0 & \ddots & 0 & \vdots \\ \vdots & 0 & \ddots & 0 \\ 0 & \cdots & 0 & 1 \\ \end{array}\right) $Wenn das amsmath-Paket eingebunden ist, stehen sechs verschiedene Matrizenumgebungen zur Verfügung. Der einzige Unterschied zwischen den Umgebungen ist die jeweilige Klammerung der Matrizen.
Ein weiterer Unterschied zur array-Umgebung ist, dass die Spaltenanzahl nicht mehr festgelegt werden muss. Die Anzahl der verwendeten Spalten wird automatisch erkannt. Im Fall, dass eine Matrix mit mehr als 10 Spalten verwendet wird, erhält man die folgende Fehlermeldung:
! Extra alignment tab has been changed to \cr.
\endtemplate
Eine mögliche Lösung ist \setcounter{MaxMatrixCols}{neuer Wert}, dadurch wird der Wert der maximalen Spaltenanzahl verändert.
Eingabe:
$\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{matrix}$
$\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}$
$\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}$
$\begin{Bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{Bmatrix}$
$\begin{vmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{vmatrix}$
$\begin{Vmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{Vmatrix}$
Ausgabe:
$\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix}$ $\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$ $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$ $\begin{Bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{Bmatrix}$ $\begin{vmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{vmatrix}$ $\begin{Vmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{Vmatrix}$Ein weiterer Unterschied zwischen den Umgebungen von amsmath und der array-Umgebung ist, dass sich die Ausrichtung der Spalten nicht ändern lässt, was aber bei der Darstellung der Einheitsmatrix nicht weiter auffällt. Ein Paket, das das Ausrichten der Spalten ermöglicht, ist das mathtools-Paket. Auf dieses Paket wird später eingegangen.
Neben den Umgebungen für normale Matrizen bietet das amsmath-Paket auch eine Umgebung an, mit der Matrizen innerhalb von Fließtext gesetzt werden können – die smallmatrix-Umgebung. Diese Umgebung bringt per se keine Klammern mit, aber wie bei der array-Umgebung können auch hier die Klammern eingefügt werden.
Eingabe:
Der Text ist $\begin{smallmatrix}
1&0\\ 0&1
\end{smallmatrix}$ nur Fassade.
Der Text ist $\bigl( \begin{smallmatrix}
1&0\\ 0&1
\end{smallmatrix} \bigr)$ nur Fassade.
Ausgabe:
Der Text ist $\begin{smallmatrix} 1&0\\ 0&1 \end{smallmatrix}$ nur Fassade. Der Text ist $\bigl( \begin{smallmatrix} 1&0\\ 0&1 \end{smallmatrix} \bigr)$ nur Fassade.Für die Auslassungen gibt es einen neuen Befehl \hdotsfor, mit dem zumindest horizontale Pünktchen gesetzt werden können.
Eingabe:
$\begin{pmatrix}
1 & 0 & \cdots & \cdots & 0 \\
0 & \ddots & \vdots & 0 & \vdots \\
\vdots & \vdots & \ddots & 0 & \vdots \\
\vdots & \vdots & 0 & \ddots & \vdots \\
0 & \cdots & \cdots & 0 & 1 \\
\end{pmatrix}$
$\begin{pmatrix}
1 & 0 & \hdotsfor{2} & 0 \\
0 & \ddots & \vdots & 0 & \vdots \\
\vdots & \vdots & \ddots & 0 & \vdots \\
\vdots & \vdots & 0 & \ddots & \vdots \\
0 & \hdotsfor{2} & 0 & 1 \\
\end{pmatrix}$
Ausgabe:
| $\begin{pmatrix} 1 & 0 & \cdots & \cdots & 0 \\ 0 & \ddots & \vdots & 0 & \vdots \\ \vdots & \vdots & \ddots & 0 & \vdots \\ \vdots & \vdots & 0 & \ddots & \vdots \\ 0 & \cdots & \cdots & 0 & 1 \\ \end{pmatrix}$ |

|
Das mathtools-Paket erweitert die Matrizenumgebungen aus dem amsmath-Paket um die Möglichkeit, dass die Ausrichtung der Spalten gesetzt werden kann. Es ist jetzt damit möglich, auch rechtsbündige oder linksbündige Spalten innerhalb der Matrizenumgebungen zu verwenden.
Der Aufbau entspricht den Umgebungen aus amsmath, aber die Namen der Umgebungen haben noch einen zusätzlichen Stern am Ende. Die gewünschte Ausrichtung wird als Option r (rechtsbündig), c (zentriert) oder l (linksbündig) übergeben. Dazu muss aber gesagt werden, dass damit immer nur alle Spalten einheitlich ausgerichtet werden können. Für den Fall, dass eine Matrix gewünscht wird, in der verschiedene Spalten eine unterschiedliche Ausrichtung besitzen, kann dies über die array-Umgebung realisiert werden.
Das mathtools-Paket bietet darüber hinaus auch Anpassungen für die Matrizen im Fließtext an.
Matrix ohne Klammern
$\begin{matrix*}[r]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{matrix*}$
|
$\begin{matrix*}[c]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{matrix*}$
|
$\begin{matrix*}[l]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{matrix*}$
|
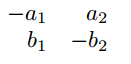 |
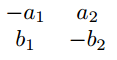 |
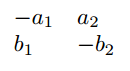 |
Matrix mit runden Klammern
$\begin{pmatrix*}[r]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{pmatrix*}$
|
$\begin{pmatrix*}[c]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{pmatrix*}$
|
$\begin{pmatrix*}[l]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{pmatrix*}$
|
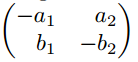 |
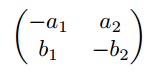 |
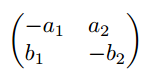 |
Matrix mit eckigen Klammern
$\begin{bmatrix*}[r]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{bmatrix*}$
|
$\begin{bmatrix*}[c]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{bmatrix*}$
|
$\begin{bmatrix*}[l]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{bmatrix*}$
|
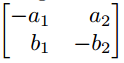 |
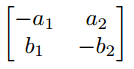 |
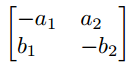 |
Matrix mit geschweiften Klammern
$\begin{Bmatrix*}[r]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Bmatrix*}$
|
$\begin{Bmatrix*}[c]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Bmatrix*}$
|
$\begin{Bmatrix*}[l]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Bmatrix*}$
|
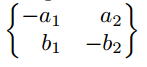 |
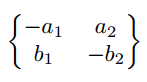 |
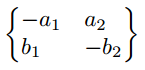 |
Matrix mit vertikalem Strich (Betragsstrich bzw. Determinantenmatrix)
$\begin{vmatrix*}[r]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{vmatrix*}$
|
$\begin{vmatrix*}[c]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{vmatrix*}$
|
$\begin{vmatrix*}[l]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{vmatrix*}$
|
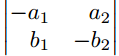 |
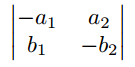 |
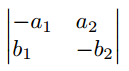 |
Matrix mit doppeltem bzw. zweifachem vertikalen Strich (Normmatrix)
$\begin{Vmatrix*}[r]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Vmatrix*}$
|
$\begin{Vmatrix*}[c]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Vmatrix*}$
|
$\begin{Vmatrix*}[l]
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Vmatrix*}$
|
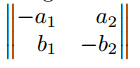 |
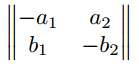 |
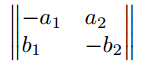 |
Das relativ neue Paket nicematrix erweitert auch die Umgebungen zur Gestaltung von Matrizen. Durch das neue Paket ist es jetzt möglich, Linien mit Pünktchen über die ganze Höhe, Breite und Diagonale einer Matrix zu setzen.
Dabei muss aber gesagt werden, dass das Paket beziehungsweise die Befehle und die Umgebungen des Pakets nicht mit allen anderen Matrizenbefehlen wie etwa \hdotsfor aus dem amsmath-Paket kombinierbar sind. Auch gibt es Einschränkungen hinsichtlich der Verwendung der neuen Befehle, wie etwa beim Befehl \Cdots, der nur zwischen zwei Spalten mit Inhalt gesetzt werden kann. Wobei der Inhalt nicht aus Pünktchen bestehen darf. Daher wurde auch im nachfolgenden Beispiel in der nicematrix-Variante zum Teil auf den Befehl \cdots zurückgegriffen.
Positiv an dem Paket ist die Darstellung der diagonalen und vertikalen Pünktchen. Und auch wenn das Paket zum jetzigen Zeitpunkt noch die eine oder andere Schwäche hat, scheint es ein sinnvoller Ansatz zu sein, um das Problem der Punkte innerhalb einer Matrix zu lösen.
Eingabe:
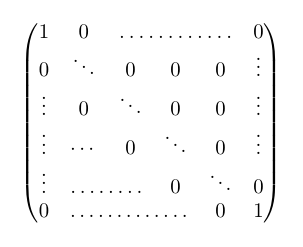
$\begin{pmatrix}
1 & 0 & \hdotsfor{3} & 0\\
0 & \ddots & 0 & 0 & 0 & \vdots \\
\vdots & 0 & \ddots & 0 & 0 & \vdots \\
\vdots & \cdots & 0 & \ddots & 0 & \vdots \\
\vdots & \hdotsfor{2} & 0 & \ddots & 0 \\
0 & \hdotsfor{3} & 0 & 1\\
\end{pmatrix} $
Ausgabe:
Eingabe:
$\begin{pNiceMatrix}
1 & 0 & \Cdots & \Cdots & \Cdots & 0 \\
0 & \Ddots & 0 & 0 & 0 & \Vdots \\
\Vdots & 0 & & 0 & 0 & \Vdots \\
\Vdots & \cdots & 0 & & 0 & \Vdots \\
\Vdots & \Cdots & \Cdots & 0 & & 0 \\
0 & \Cdots & \Cdots & \Cdots & 0 & 1 \\
\end{pNiceMatrix} $
Ausgabe: