 Befehle
Pakete
Klassen
Strukturen
Fehlermeldungen
Befehle
Pakete
Klassen
Strukturen
Fehlermeldungen
Das amsmath Paket (v2.15a 2016) gehört zu den absoluten Standardpaketen in LaTeX da es eine Vielzahl von neuen Umgebungen und Befehlen für den mathematischen Bereich beinhaltet. Das Paket selbst ist Teil einer ganzen Paketereihe zum Themenbereich Mathematik. Eine gute Übersicht zu dem Paket insbesondere im Vergleich mit den Möglichkeiten die mit LaTeX Standard Befehlen möglich sind bietet Mathematischer Satz mit dem Paket amsmath von Günter Partosch.
Das Paket selbst bindet noch weitere Pakete aus der AMS Reihe (amstext, amsbsy und amsopn) ein.
Das Paket verfügt über 12 Optionen von denen fünf automatisch gesetzt sind. Diese wurden mit default gekennzeichnet und sind fett geschrieben:
centertags (default) Sorgt bei Gleichungen innerhalb der split Umgebung dafür, dass die Gleichungsnummer vertikal zentriert im Bezug auf die Höhe der Gleichung dargestellt wird.
tbtags Sorgt bei Gleichungen innerhalb der split Umgebung dafür, dass die Gleichungsnummer an der letzten (bzw. ersten) Zeile ausgerichtet wird, wenn die Nummer auf der rechten (bzw. linken) Seite sind.
sumlimits (default) Innerhalb von abgesetzten Gleichungen werden beim Summenzeichen der Laufindex und die Grenze über das Symbol gesetzt. Ebenso wie bei anderen Symbolen dieses Typs, mit Ausnahme des Integrals.
nosumlimits Wird diese Option gesetzt wird auch innerhalb einer abgesetzten Gleichungsumgebung, der Laufindex und die Grenze neben dem Summenzeichen gesetzt. Dies gilt auch für die anderen Symbole dieses Typs.
nointlimits (default) Innerhalb von abgesetzten Gleichungen werden beim Integralzeichen die untere und obere Schranke neben das Zeichen gesetzt.
intlimits Wie sumlimts nur diesmal für das Integralzeichen.
namelimits (default) Gleiche Effekt wie sumlimits, nur bezieht es sich auf die Funktionen die über eine limits verfügen wie etwa min und max im Fall, dass eine abgesetzte Gleichung verwendet wurde.
nonamelimits Das Gegenteil von namelimits.
leqno Platziert die Nummerierung links von der Gleichung.
reqno (default) Platziert die Nummerierung rechts von der Gleichung.
fleqn Richtet die Gleichung linksbündig aus anstelle von zentriert, wie die entsprechende Dokumentenklassenoption.
cmex10 Diese Option hat heutzutage keine Bedeutung mehr.
In diesem Abschnitt werden die ausgewählte neuen Befehle kurz vorgestellt. Um die Beispiel realistischer zu gestalten wurde gelegentlich auch das Paket amssymb mitverwendet.
text
Mit Hilfe des Befehls \text{Inhalt} kann innerhalb einer Matheumgebung normaler Text geschrieben werden.
Seien $a,b \in \mathbb{R},
\text{ dann gilt } (a+b)^{2} = a^{2} + 2ab + b^{2}$\\
Seien a,b ∈ ℝ , dann gilt (a + b)Ein ähnlicher Befehl ist \intertext{Inhalt} wobei dieser zumeist innerhalb von Gleichungen zu Einsatz kommt. Zudem erfordert intertext einen vorausgehenden Zeilenumbruch und es kann unter Umständen zu einem Seitenumbruch kommen.
\begin{align*}
a - b &\geq 0 \text{ wenn } b \leq a \\
\intertext{ andernfalls gilt }
a -b &< 0
\end{align*}
a − b ≥ 0 wenn b ≤ a Für den Fall, dass gezielt an einer bestimmten Stelle ein Seitenumbruch, innerhalb einer Gleichungsumgebung gesetzt werden soll, wird der Befehl \displaybreak[Option] verwendet. Die Option kann dabei einen Wert von 0 bis 4 besitzen, wobei der Defaultwert 4 beträgt und je höher der Wert desto wahrscheinlicher wird der Seitenumbruch umgesetzt. Bei der Wirkung des Befehls muss aber beachtet werden, dass er sich auf den nächsten Zeilenumbruch (\\) bezieht.
& ...
{\sigma^{2}_{1} \sigma^{2}_{2}
\sigma^{2}}\right)\right)dv\\ \displaybreak
&=\frac{1}{2 \pi \sigma_{1} \sigma_{2}}
\int^{\infty}_{-\infty} \exp \left(-\frac{1}{2}\left(
...
\right)\right)dv\\
Operator
Das Pakete bietet auch die Möglichkeit neue eigene Operatoren zu definieren. Dabei gibt es zwei Varianten. Die erste ist der Befehl \operatorname{Neuer Operator} damit wird einmalig der Operator gesetzt. Die zweite Variante mit dem Befehl \DeclareMathOperator{\NeuOp}{Neuer Operator} erstellt einen dauerhaft in diesem Dokument verwendbaren neuen Operator.
Einmalig: \operatorname{NeuerOperator}
Neuer Operatorbefehl: \DeclareMathOperator{\NeuOp}{NeuerOperator}
Amsmath enthält auch zwei Schriftvarianten, um Symbole fett schreiben zu können. Die erste Variante ist \boldsymbol{ Symbole und Variablen fett} und die zweite Variante ist \pmb{Symbole und Variablen sehr fett} die Varianten unterscheiden sich nicht nur im Grad der Stärke voneinander, sondern auch wie sie mit dem Befehl \text{Inhalt} verfahren. Die boldsymbol Variante bezieht sich nur auf die Symbole und Variablen, während pmb alles, also auch denn normalen Text fett schreibt.
Eingabe
Seien $\boldsymbol{a,b \in \mathbb{R}, \text{ dann ist }
(a+b)^{2} = a^{2} + 2ab + b^{2}}$\\
Seien $\pmb{a,b \in \mathbb{R}, \text{ dann ist }
(a+b)^{2} = a^{2} + 2ab + b^{2}}$\\
Ausgabe:
Seien a,b ∈ ℝ , dann gilt (a + b)
Seien a,b ∈ ℝ , dann gilt (a + b)
Wenn das mathptmx (New Times Roman Schrift) verwendet wird, sollte das eucal Paket eingebunden werden, wenn kalligraphische Schrift verwendet wird.
GrößenanpassungenFür die displaystyle und textstyle Größen gibt es für den Bruch und den Binom Befehl eine abkürzende Schreibweise, sodass Konstruktion wie etwa {\displaystyle \frac ...} überflüssig werden.
| $\dfrac{1}{\dfrac{a}{b}}$ |
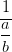
|
|||||
| $\tfrac{1}{\tfrac{a}{b}} $ |
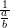
|
|||||
| $\dbinom{n}{k} = \dbinom{n-1}{k-1} +\dbinom{n-1}{k}$ |
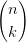 | = | 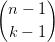 | + | 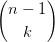
|
|
| $\tbinom{n}{k} = \tbinom{n-1}{k-1} +\tbinom{n-1}{k}$ |
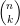 | = | 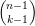 | + | 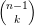
|
Die fehlenden Größenanpassungen, für scriptstyle und scriptscriptstyle, lassen sich über den Befehl genfrac selbst erstellen.
\newcommand{\sfrac}{\genfrac{}{}{}2}
\newcommand{\ssfrac}{\genfrac{}{}{}3}
$\sfrac{a}{b}$ und $\ssfrac{a}{b}$ 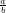 und
und 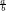
\newcommand{\sbinom}{\genfrac(){0pt}2}
\newcommand{\ssbinom}{\genfrac(){0pt}3}
$\sbinom{n}{k}$ und $\ssbinom{n}{k}$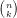 und
und 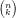
Nachfolgend eine kurze Übersicht über die neuen Befehle und Umgebungen.
Binom$\binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}$
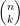 | = | 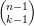 | + | 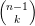 |
$\cfrac{1}{\cfrac{a}{b}}$
$\sqrt{2} = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{1 + \sqrt{2}}}}}$
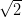 | = 1 + | 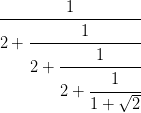 |
$A \overset{!}{=} B$ A 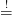 B und
$A \underset{!}{=} B$ A
B und
$A \underset{!}{=} B$ A 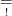 B
B
$A \xleftarrow[unten]{oben} B$
$A \xrightarrow[unten]{oben}B$
$A \xleftarrow{\text{links}} B \xrightarrow[\text{oder rechts}]{} C $
$\overrightarrow{\text{Pfeil oben Rechts}}$

$\overleftarrow{\text{Pfeil oben Links}}$

$\overleftrightarrow{\text{Doppelpfeil oben}}$

$\underrightarrow{\text{Pfeil unten Rechts}}$

$\underleftarrow{\text{Pfeil unten Links}}$

$\underleftrightarrow{\text{Doppelpfeil unten}}$

$\sum_{\substack{0 \leq 1 < m\\ 0 < j < n}} a(i,j) $ ∑
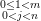 a(i,j)
a(i,j)
$\sum_{\begin{subarray}{l} 0 \leq 1 <m\\ 0<j<n\end{subarray}} a(i,j)$
∑
$f(x) = \begin{cases}
5 & x \geq 0 \\
23 & \, \text{sonst}
\end{cases}$
| f(x) = |
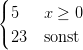
|
\boxed{x-y \leq 0 \to \forall \,x\in \mathbb{R} y \geq x}
x - y ≤ 0 → ∀ x ∈ ℝ y ≥ xAuslassungen und Abstände
$, \dotsc , $ … Kommapunkte
$+ \dotsb +$ +⋅⋅⋅+ Operatorenpunkte
$\cdot \dotsm \cdot $ ⋅⋅⋅ Multiplikationspunkte
$\int \dotsi \int$ ∫ ⋅⋅⋅ ∫ Integralpunkte
$\dotso $ … Punkte
Punkte über ∑
$\dddot \sum $ |
|
$\ddddot \sum $ |
|
Punkte innerhalb einer Matrix.
\hdotsfor{Spaltenzahl Punkte}
\[\begin{matrix} a&b&c&d&e\\
e&\hdotsfor{3}& 1 \end{matrix}\]
Ausgabe:
| Abk. | Befehl | Beispiel |
| $A B$ | AB | |
| \, | $A\thinspace B$ | AB |
| \: | $A\medspace B$ | A B |
| \; | $A\thickspace B$ | A B |
| $A\quad B$ | A B | |
| $A\qquad B$ | A B |
| Abk. | Befehl | Beispiel |
| $A B$ | AB | |
| \! | $A\negthinspace B$ | AB |
| $A\negmedspace B$ | AB | |
| $A\negthickspace B$ | AB |
eigener Abstand: \mspace \mspace{-18.0mu} = -\quad
Allgemeine Hinweise:
\begin{Name}
a_{2} \ldots x^{5}
\end{Name}
ohne Nummerierung:
\begin{Name*}
a_{2} \ldots x^{5}
\end{Name*}
equation Einzeilige Gleichungsumgebung
\begin{equation}
a = b
\end{equation}
|
a = b | (1) |
|
|
|
\begin{align} a &= b + c \\ c &= e \end{align} |
|
\begin{align*}
a_{11} &= b_{11} & a_{12} &= b_{21} & a_{13} &= b_{31}\\
a_{21} &= b_{12} & a_{22} &= -b_{22} & a_{23} &= b_{32}
\end{align*}
| a11 = b11 | a12 = b21 | a13 = b31 | ||
| a21 = b12 | a22 = -b22 | a23 = b32 |
|
\begin{flalign} a &= b + c \\ c &= e \end{flalign} |
|
\begin{flalign}
a_{11} &= b_{11} & a_{12} &= b_{21} & a_{13} &= b_{31}\\
a_{21} &= b_{12} & a_{22} &= -b_{22} & a_{23} &= b_{32}
\end{flalign}
| a11 = b11 | a12 = b21 | a13 = b31 | ||
| a21 = b12 | a22 = -b22 | a23 = b32 |
Die erste Zeile ist linksbündig, die letzte rechtsbündig und die Zeilen dazwischen sind zentriert.
\begin{multline}
L + S = e + r + s \\
+ zw + re + se \\
+ dri + rec + sei\\
+ vier + rech + seit \\
+ fuenf + recht + seite \\
+ sechst + rechte + seite\\
+ letzte + zeile
\end{multline}
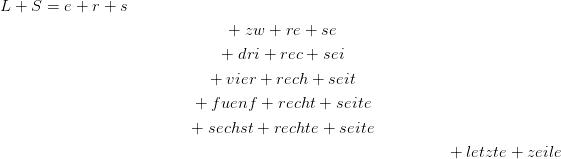 | (1) |
Manueller Umbruch innerhalb von Gleichung, aber Achtung die Umgebung funktioniert nicht innerhalb der multline Umgebung.
\begin{equation}\begin{split}
H_c&=\frac{1}{2n} \sum^n_{l=0}(-1)^{l}(n-{l})^{p-2}
\sum_{l _1+\dots+ l _p=l}\prod^p_{i=1} \binom{n_i}{l _i}\\
&\quad\cdot[(n-l )-(n_i-l _i)]^{n_i-l _i}\cdot
\Bigl[(n-l )^2-\sum^p_{j=1}(n_i-l _i)^2\Bigr].
\end{split}\end{equation}
![n p ( )
1--∑ l p− 2 ∑ ∏ ni
Hc = 2n (− 1) (n − l) li
l=0 l1+⋅⋅⋅+lp=li=1 p
ni−li 2 ∑ 2
⋅ [(n − l) − (ni − li)] ⋅ [(n − l) − (ni − li) ].
j=1](AMS39x.png) | (1) |
\begin{subequations}
\begin{align}
\sum_{i=0}^{n} a_{i} = & \ldots \\
\prod_{i=0}^{n} a_{i} = & \ldots
\end{align}
\end{subequations}
| ∑i=0n ai | = | … | (1a) |
| ∏i=0n ai | = | … | (1b) |
|
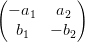
|
![[ ]
− a1 a2
b − b
1 2](AMS41x.png)
|
||||||
$\begin{matrix}
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{matrix} $
|
$\begin{pmatrix}
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{pmatrix} $
|
$\begin{bmatrix}
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{bmatrix} $
|
||||||
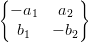
|
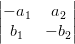
|
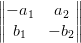
|
||||||
$\begin{Bmatrix}
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Bmatrix} $
|
$\begin{vmatrix}
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{vmatrix} $
|
$\begin{Vmatrix}
-a_{1} & a_{2} \\
b_{1} & -b_{2}
\end{Vmatrix} $
|
Die folgende Fehlermeldung erscheint, wenn mehr wie 10 Spalten innerhalb einer Matrix Umgebung verwendet wurden.
! Extra alignment tab has been changed to \cr. \endtemplateMögliche Lösung: \setcounter{MaxMatrixCols}{neuer Wert}Dadurch kann der Wert entsprechend erhöht werden. Matrizen im Text
Der Text ist $\begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} $ nur Fassade.
| Der Text ist |
|
Der Text ist $\bigl( \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} \bigr)$ nur Fassade.
| Der Text ist |
|
Der Text ist $\bigl[ \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} \bigr]$ nur Fassade.
| Der Text ist |
|
Der Text ist $\bigl\{ \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} \bigr\}$ nur Fassade.
| Der Text ist |
|
Der Text ist $\mid \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix}\mid$ nur Fassade.
| Der Text ist |
|
Der Text ist $\bigl\| \begin{smallmatrix}
a&b\\ c&d
\end{smallmatrix} \bigr\|$ nur Fassade.
| Der Text ist |
|